Разработан дополнительный модуль расчета функции близости для многослойных подложек методом Монте Карло

May 25, 2009

Создан дополнительный модуль для расчета функции близости для многослойных подложек. Расчет производится методом Монте-Карло. Полученное распределение поглощенной энергии (дозы) в резисте подгоняется двумя гауссианами, параметры которых меняются по глубине. Новый параметр - ₀, добавлен к параметрам функции близости, который позволяет учитывать изменения дозы по глубине резиста. Рассчитанные методом Монте-Карло данные, наряду с экспериментальными данными, используются в качестве рекомендованных параметров при экспонировании, коррекции эффекта близости и моделировании проявления резиста.

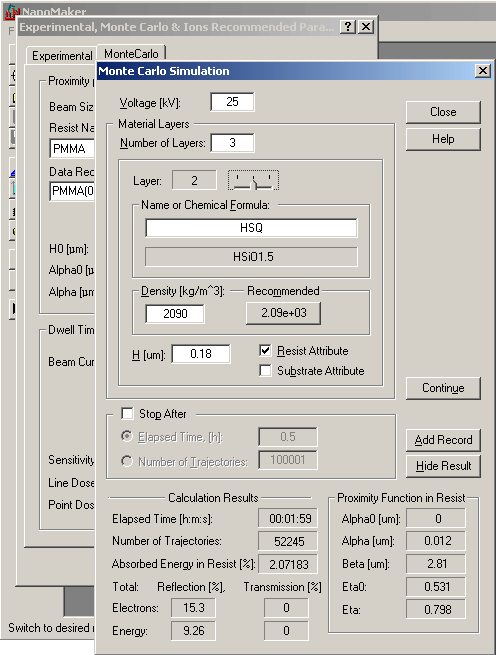
Диалоговое окно используется для установки исходных параметров и для запуска расчета распределения поглощенной энергии после рассеяния электронов в многослойной мишени. Первичный электронный пучок падает (перпендикулярно плоскости XY слоев) и имеет нулевой размер (диаметр). Нумерация слоев начинается на поверхности от точки падения пучка и продолжается вглубь мишени. Самый верхний слой имеет номер 1, самый глубокий слой имеет наибольший по порядку номер. До 20 слоев может быть определено таким образом.
Метод Монте-Карло используется для моделирования большого числа траекторий электронов. Алгоритм использует рассеяние Резерфорда на экранированных ядрах и приближение непрерывного замедления для расчета потерь энергии вдоль траектории движения электронов [1]. Потерянная энергия аккумулируется в ячейках расчетной сетки. Сетка имеет цилиндрическую симметрию в XY плоскости с центром на оси пучка электронов и нерегулярна вдоль радиуса и в Z направлении. Это способствует ускорению расчетов, позволяя рассчитать 50000 траекторий за 2 мин в простой системе - резист на кремниевой подложке (ускоряющее напряжение - 25 кВ; толщина ПММА резиста - 0.5 мкм; Si подложка) на Intel Core Duo CPU. Такого количества траекторий обычно достаточно для расчета параметров функции близости.

Один из слоев мишени должен быть отмечен как резист. Распределение энергии в слое это искомая функция близости I(x,y,z) для коррекции эффекта близости и моделирования проявления резиста.

Где = 3.1415…. Распределение энергии, аккумулированное в расчетной сетке, подгоняется по формуле с использованием линейной аппроксимации для (z) (₀=(H) на верхней границе резиста, - на нижней границе резиста). ²(z)= ₀²+( ²-₀²)*( 1-z/H )³, где z - расстояние от нижней границы резиста. Пять параметров: ₀, , , ₀, определяют функцию близости для моделирования эффекта близости. Три параметра: , , определяют функцию близости для коррекции эффекта близости.

[1] L. Reimer "Scanning Electron Microscopy. Physics of Image Formation and Microanalysis" Second Edition Springer Series in Optical Sciences Vol. 45, 1998

Назад к Новостям